Clustering With K-Means in Python | The Data Science Lab

Clustering With K-Means in Python | The Data Science Lab

The k-means algorithm takes a dataset X of N points as input, together with a parameter K specifying how many clusters to create. The output is a set of K cluster centroids and a labeling of X that assigns each of the points in X to a unique cluster. All points within a cluster are closer in distance to their centroid than they are to any other centroid.

The mathematical condition for the K clusters 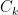 and the K centroids  can be expressed as:

Minimize  with respect to .

In practice, the algorithm is run multiple times and averaged.

Finding the solution is unfortunately NP hard. Nevertheless, an iterative method known as Lloyd’s algorithm exists that converges (albeit to a local minimum) in few steps. The procedure alternates between two operations. (1) Once a set of centroids  is available, the clusters are updated to contain the points closest in distance to each centroid. (2) Given a set of clusters, the centroids are recalculated as the means of all points belonging to a cluster.

The two-step procedure continues until the assignments of clusters and centroids no longer change. As already mentioned, the convergence is guaranteed but the solution might be a local minimum. In practice, the algorithm is run multiple times and averaged. For the starting set of centroids, several methods can be employed, for instance random assignation.

Read full article from Clustering With K-Means in Python | The Data Science Lab